When making a top-down 2D game, you might be tempted to implement 8 directional movement in a naive way resulting in the player moving faster diagonally.
The goal of this post is to explain how to make sure that the speed of a player’s diagonal movement is the same as moving in only one direction.
We’ll be doing this in JavaScript using the Kaplay (Formerly known as Kaboom) library. I assume that you have basic knowledge of Kaplay. If you’re interested in learning the library, you can head over to my YouTube channel where I have many project based tutorials or you can check the official docs.
The Naive Approach
Earlier I mentioned a naive approach to implementing 8 directional movement. Here is what it looks like in code. We’ll discuss why the player moves faster diagonally with this setup.
import kaplay from "kaplay"
const k = kaplay()
k.loadBean()
const player = k.add([
k.sprite("bean"),
k.pos(k.center()),
{
speed: 300
}
])
player.onUpdate(() => {
if (k.isKeyDown("left")) player.move(-player.speed, 0)
if (k.isKeyDown("right")) player.move(player.speed, 0)
if (k.isKeyDown("up")) player.move(0, -player.speed)
if (k.isKeyDown("down")) player.move(0, player.speed)
})You should obtain the following behavior. Here, you’ll notice that you move slightly faster diagonally.
Why is that? It can be explained with a bit of math.
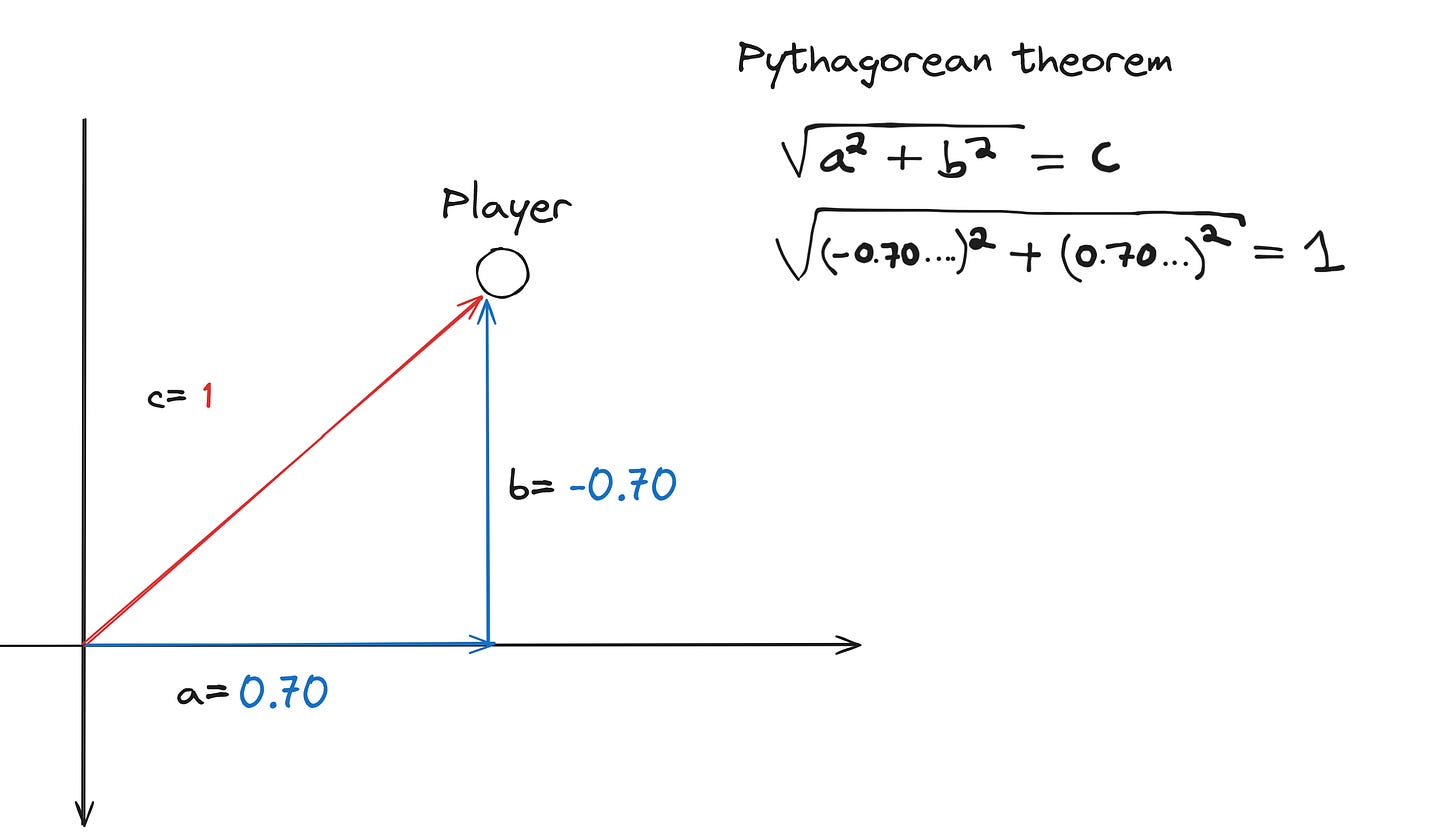
For example, when you press both the right and up keys, the player will move at a speed of 300 on the x axis (represented by the blue vector a) and at a speed of 300 on the y axis (represented by the blue vector b).
Since the player diagonal movement vector c is composed of these two vectors (a and b) and forms a right triangle, we can use the Pythagorean theorem to calculate the speed the player will move at diagonally. The result obtained is 424.26 which is above the speed you would get by moving only in one direction.
The Solution
To make the player move at the same speed diagonally as they would in a single direction, we need to normalize our vectors. This means that we want all of our vectors to have a length of 1 (otherwise known as a unit vector) while retaining each vectors’ direction. Visually it would look like this.
We will later scale the vectors by the speed (300 in our example) so that the player moves at that speed instead of 1. Normalizing will make sure that when the player presses both keys (for example : right and up) the resulting vector will be of length 1 instead of being slightly longer due to the nature of right triangles. So it’s as if all vectors are now going to be constrained within a circle with a radius of 1.
Here is the code for this :
import kaplay from "kaplay";
const k = kaplay()
k.loadBean()
const player = k.add([
k.sprite("bean"),
k.pos(k.center()),
{
speed: 300
}
])
player.onUpdate(() => {
const directionVector = k.vec2(0, 0)
if (k.isKeyDown("left")) directionVector.x = -1
if (k.isKeyDown("right")) directionVector.x = 1
if (k.isKeyDown("up")) directionVector.y = -1
if (k.isKeyDown("down")) directionVector.y = 1
const unitVector = directionVector.unit(); // make sure that the vector has a magnitude of 1
player.move(unitVector.scale(player.speed));
})Here, we first compute our direction vector and then we normalize it by using the unit() Kaplay method.
So when we move diagonally (for example up and to the right) our direction vector will be (-1, 1) before normalization. (-1 because in gamedev to go up you need to reduce the value of y since the Cartesian plane is inverted)
By applying the unit() method on this vector we get (-0.70…, 0.70…) which is what we need since if we use the Pythagorean theorem with these values we will obtain a length of 1 for the diagonal vector which is what we want.
Finally, we scale the unit vector we just obtained by the speed using Kaplay’s scale() method and we’re good to go.
A More Efficient Way
Since a^2 + b^2 is always equal to 2 for a diagonal, we therefore know that sqrt(a^2 + b^2) is always equal to sqrt(2). We can deduce that any diagonal is always a factor sqrt(2) longer than the horizontal or vertical direction. To achieve the same behavior we had earlier, we only need to multiply by 1 / sqrt(2) when the player moves diagonally. No need for extra calculations since we can use 1 / sqrt(2) as a constant.
The code looks like this :
const diagonalFactor = 1 / Math.sqrt(2);
k.onUpdate(() => {
const directionVector = k.vec2(0, 0);
if (k.isKeyDown("left")) directionVector.x = -1;
if (k.isKeyDown("right")) directionVector.x = 1;
if (k.isKeyDown("up")) directionVector.y = -1;
if (k.isKeyDown("down")) directionVector.y = 1;
// this is true when the player is moving diagonally
if (directionVector.x && directionVector.y) {
this.move(directionVector.scale(diagonalFactor * this.speed));
return;
}
this.move(directionVector.scale(this.speed));
});Conclusion
If someone asks you : “When will we ever use the Pythagorean theorem in real life?”
Well, you have something to show them ;)
To be notified when I publish more posts like this, subscribe!
Here are a few other posts you can read if you want.
How to Implement a Zelda Link's Awakening Style Camera in Kaplay
Zelda Link’s Awakening has a camera that behaves like shown below. Let’s implement it in Kaplay.
How to implement player controls for a 2D top-down mobile web game in Kaboom.js
I make JavaScript (Kaboom.js) game programming tutorials on YouTube. Check my channel here. Let’s assume you’re making a 2D top-down game and you want it playable on both desktop and mobile. The most sensible choice for a player control scheme would be to implement a touch/click around to move controller.